虽然我们有了API可以进行一定的数据预处理,但是,拿到一个数据集后,我们第一想到的就是先进行处理吗?要把数据集里面的每个维度都去压缩吗?每个维度要用什么方式去压缩呢?
相关度计算
你首先肯定是知道你需要研究什么的,比如我的研究的就是我的会员有没有付费买东西的可能,而我的数据库里,一条会员的数据就有几十个属性,是不是每个属性都要拿出来,每个属性和会员的质量关系有多大呢?
一般来说根据最终使用的算法的不同,研究对象的不同,根据实际情况,算出相关度后,保留前N个属性做为研究就够了,不需要把所有的属性都带上。
协方差
最简单的计算方式莫过于协方差了,一行np.cov就可以搞定,对于数值型数据的相关性,也可以用协方差来计算。
相关系数
如果不怕累,可以把所有的属性都二二结对生成散点图,但计算出来,直接给出相关性最高的几组数据不是更好,相关度之前在统计的笔记里面就已经提到了,这里再提一次,公式:
$$r_{A,B}=\frac{\sum_{i=1}^n (a_i-\overline{A})(b_i-\overline{B})}{n\sigma_A\sigma_B} = \frac{\sum_{i=1}^n (a_ib_i) - n \overline{A} \overline{B} }{n\sigma_A\sigma_B}$$
相关系数的值在-1到1之间,为正则正相关,负则负相关,值越大则相关性越强,为0的时候,则A和B不具有线性相关性,并非A和B不相关。当然了我们大多数研究都是线性的,所以我们算出为0的数不想继续深入的时候,就可以放弃了(直接认为不相关),项目中,原则为基础,先粗后细,避免把大量时间浪费在性价比低的小优化上。
卡方
相关系数只能处理数值型数据,对于类型数据(标称数据),的相关系数:可以用卡方检验,公式如下:
$$x^2 = \sum^{c}{i=1} \sum^{r}{j=1} \frac{(o_{ij}-e_{ij})^2}{e_{ij}}$$
其中,o(ij)为实际计数,e(ij)为期望计数,e(ij)可以用公式计算
$$e_{ij} = \frac{count(A = a_i) * count(B = bj)}{n} $$
光看公式肯定是不够的,照套一个例子说明一下,不够生动,不懂的最好自己再去找资源搞懂: 以下数据是对300的男生和1200个女生发起的一份调查报告,喜欢看小说类的书或是非小说类的书,结果
| 男 | 女 | 合计 | |
|---|---|---|---|
| 小说类 | 250(90) | 200(360) | 450 |
| 非小说类 | 30(210) | 1000(840) | 1050 |
| 合计 | 300 | 1200 | 1500 |
这张表和统计里面的交叉表一样,不同点有个括号,括号里面的数是怎么来的,先看合计最后一列,1500人里面450人喜欢小说类,1050人喜欢非小说类,那么,认为性别无关情况下,在男女生中都应该是450:1050。所以期望男生喜欢小说类的人数应该为 300 * 450 / 1050 = 90人,实际为250人。
然后将e(ij)代入上面的公式一算,可以看出结果为507.63。这个值怎么用呢,还是统计的知识,在0.001的置信水平下,要想拒绝假设要达到10.828。基本可以直接判定性别与喜好是强相关的。
特征选择
数据挖掘过程中,肯定不是属性越多越好,做什么样的研究,选什么样的属性,常见的研究一个人的收入,肯定就会选择年龄、学历、职业、职位等,对于身高、联系方式、颜值等属性可能就不需要过多关注,当然做一些其它研究时可能就恰恰相反。
特征选择也是预处理的重要一环,可以降维、大大减少计算量,将不相关的属性(列)清理出去。比较直观的方法就是直接用工具画一个属性 - 分析目标的分布图,相交部分越少,则属性越理想,相交部分多则表示并没在什么卵用,随手画一个:
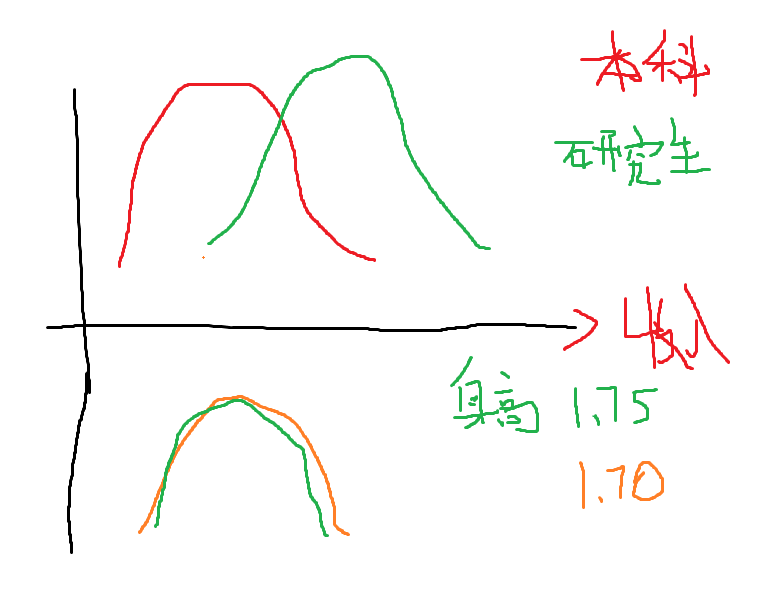
不确定性 Entropy
不确定性,是后续做决策树算法的一个基础知识(从思想上感觉和贝叶斯一样),还是上面的例子:已知收入分布如下:
| 收入 | 比例 |
|---|---|
| 低 | 50% |
| 高 | 50% |
求熵公式:
$$H(X)= - \sum^n_{i=1}p(x_i)log_bp(x_i)$$
对于上面的0.5:0.5,用求熵公式计算:$H(S)= -0.5 * log_2 0.5 - 0.5 * log_2 * 0.5 = 1$
即不确定性为1,最不确定(当概率为0.5的时候,熵是最高的),如果按上面的概率随便给个人猜收入是高是低,那么只能瞎猜了,当低:高 = 0:1的时候,熵为0,即不确定性为0,就是完全确定,再猜就不用乱猜了。
信息增益
当我知道了这个的学历是研究生之后,(假设已知研究生的收入低:高 = 0.2:0.8,非研究生的收入低:高=0.95:0.05),那么这个时候再让我去猜这个人的收入是高是低,那我肯定会猜收入会高,猜对的几率是80%了嘛。
其实,把这两个代入求熵公式一算,可以求出已和研究生的不确定性有0.7219,非研究生的不确定性有0.2864,那么把0.7219 - 0.2864 = 0.5447,则为知道学历属性后不确定性。
用整体不确定性 - 学历不确定性 1-0.5447 = 0.4523,则为 信息增益。
信息增益:当我知道了一个属性后,我对整体的不确定性降低了多少,越大越好。
剪枝
熟悉数据结构的程序员们对剪枝可能已经有所了解了,在数据挖掘里面小提一下,是因为数据挖掘里面有场景可以很好的使用剪枝算法来大大减少计算量。
比如一个数据表里面有20个属性,考虑到计算成本,只想选择最好的5个属性做挖掘分析,怎么找到这5个属性。如果不用减枝算法,用概率组合公式计算,我需要遍历出15504种不同的组合,然后寻找最优解,如果仅是简单计算1W多次计算侄是是个小Case,但每种组合我们要求的是信息增益量,又涉及到很复杂的计算,估计够呛。
具体的剪枝算法可以去自行Google,对于程序员们来说应该不难理解,由于在数据挖掘中,[A,B,C]的组合是[A,B,C,D]的子集,子集的信息增益量可以想像为是父集的一部分,那么对[A,B,C]> [D,E,F,G,I]这样的结点来说,整个[D,E,F,G,I]都可以从树上剪掉了,所有子集都不需要遍历了。
当然,除了剪枝还有很多算法可以做属性组合选择,比如简单的快速序列算法、竟技搜索、遗传算法等等。
数据归约
对于数据归约,主要有PCA(主成份分析)与LDA(线性判别分析)方法,由于篇幅问题,不作详细说明,而且目前感觉不知道应用场景,先搁在这,后续想到了再补充这里。
PCA可以把多维空间的数据投影到一维或二维的空间里面,简化数据处理。
但如果数据里面有分类成簇,那么PCA肯定就不适用了,可以用LDA去处理,实际上也可以用LDA做一个线性分类器。对于 PCA,LDA,各种软件包的API里面都有相关的API,不用自己再去写方法去计算。
抽样
统计中也有抽样的介绍,与统计不同的是,统计的瓶颈在于数据的收集上,不能去统计所有的人,所以对受访者做抽样进行统计。数据挖掘的瓶颈在计算上,数据太多了,对于在万级以上的数据量,如果把要所有的数据拿出来做简单的平均、方差计算,还免强OK,做要做挖掘分析,维度运算,再强悍的计算机也不够。
并不是说大数据技术就是把所有的数据都进行处理,很多时候,你只要从数据库中取到5%的数据进行分析,可以达到几乎和100%的数据一样的效果,节省了时间与机器,何乐而不为。
- 对于太详细的信息,不需要太多关注,可以先Group By,拿一个统计,可以大大减少数据量
- 对于不平衡数据,最好是有意的一样取一点,比如某理工大学男女比例为9:1,那么最好多抽点女生,少抽点男生,对分析有一定好处。
- 对于不同的场景,可以使用不同的抽样方法,如簇抽样、分层抽样、等等,可降低一定的复杂度。
另外,对于不平衡数据,最好不要用简单的命中率来度量算法的好坏,比如A:B=99:1的数据,做了个分类器全部分类为A,得出结果为命中率99%,然而并没有什么卵用。
可以使用以下度量方法,具体公式也比较简单,可以自行搜索:
G-mean :
考虑分类A上的准确率乘以B分类的的准确率,比如上面A的准确率为100%,B的准确率为0,相乘还是0,所以按一般算法命中率99%相当不错的其实按G-mean并没卵用。F-measure :
和G-mean比较类似,考虑准确度以及招回率,考虑两类问题的准确率。一般在搜索引擎中用的比较多。
小结
数据预处理就到这了,数据预处理的重要性可以说比数据挖掘本身还高,如果数据预处理没做好,后续分析出的模型可能都是不准确的,往往造成返工重干。另外还有一点,可能在文章中说了很多遍了,数据挖掘灵活性很高,不像做传统软件,不确定因素也比较多,所以定制性也比较高,基本没有一棒通吃的算法,都是要根据实际场景去解决实际问题。