今天主要总结一下最基础的公式,基本上都是书上照搬,统计的基本公式最重要的作用就是后续做区间估计,方差分析,线性回归等实际应用场景,当然了,就算对统计皮毛都不知道的人都知道一些基本的,比如平均数等。
对于大学贡献给网游的本人来说,只能勤练反补了,主要门槛也就两点:一个是英语要OK,做为最终需要应用落实来说,程序的变量总要会写、Google上的关键字总要会打吧。另外就是数学要OK,后面的很多概率公式、分布函数等等都需要有高数基础,不过数学不是必选项,它会告诉你公式的演绎原理让你更为深入的理解,当然如果没有可以直接应用于各种分析,但对于复杂的问题可能会遇到瓶颈,所以不懂高数的,学完后再补习一下大学课本也是个不错的选择。
平均数(mean)、中位数(median),众数(mode)
在概念上,平均数分为样本平均数与总体平均数,实际上算法都是一样的,但在统计上,后续算一些其它的变量时需要分开,$\mu$是后续非常用的一个变量。
样本平均数: $\overline{x} = \frac{\sum_{x_i}}{n} $
总体平均数: $\mu = \frac{\sum_{x_i}}{N} $
中位数:是奖数据按从小到大排列后,最中间的一个数(奇数个)或最中间两个数的平均数(偶数个)。
众数:是出现在一组数据里面次数最多的那个数。
这三个数都是用来描述一组数的状况的(集中趋势),有的时候,平均数不是太好反映真实数据的时候,可以用中位数用来描述平均数(average)比如,以下是我们公司10个人的工资[2500,3000,3000,3500,3800,4000,4500,4500,5000,1000000],当然了,一百万的工资是BOSS的,那就可以得出我们公司的平均工资是10W+?即使是真的,会有人信?这时可以用中位数来描述,即平均为3900。
numpy里面有相关的方法,pandas里面应该也有,其实一般根据英文单词就可较快找到相应的api,只要在ipython环境里面打出np.me,再几个tab就出来啦。
| 平均数1 | np.mean() |
| 平均数2 | np.average() |
| 中位数 | np.median() |
极差(range)、方差(variance)、标准差(standard deviation)、标准差系数(coefficient of variation)
- 极差 : 最大值 - 最小值
- 总体方差 : $\sigma^2 = \frac{\sum(x_i-\mu)^2}{N} $
- 样本方差 : $s^2 = \frac{\sum(x_i-\overline{x})^2}{n-1} $
- 样本标准差 : $s = \sqrt{s^2} $
- 总体标准差 : $\sigma = \sqrt{\sigma^2} $
- 标准差系数 : $(\frac{标准差\sigma }{平均数\overline{\mu}}\times{100} ) % $
| 极差 | 内置方法都可以:max(data)-min(data) |
| 总体方差 | np.var()、nanvar() |
| 样本方差 | np.var(ddof=1) |
| 总体标准差 | np.std() |
| 样本标准差 | np.std(ddof=1) |
| 标准差系数 | np.std(dof=1)/np.mean() |
概念性的东西不多解释。方差、标准差用于计算变异程度,后续用来做分布函数、各种检验,实验都是非用不可的。这些都是表示数据变异性的,通常来说,市面上很喜欢拿异端说事,比如大家都能知道创业成功的前辈名字,说起谁谁谁赚多少多少的,而实际上创业的人实在太多,真正成功的确较少,大多数平常的创业者们当然没法引起市场关注了,很多创业者都是亏损的情况就更不用说,但市场仅喜欢讨论异端,所以给人的感觉就像创业很简单。
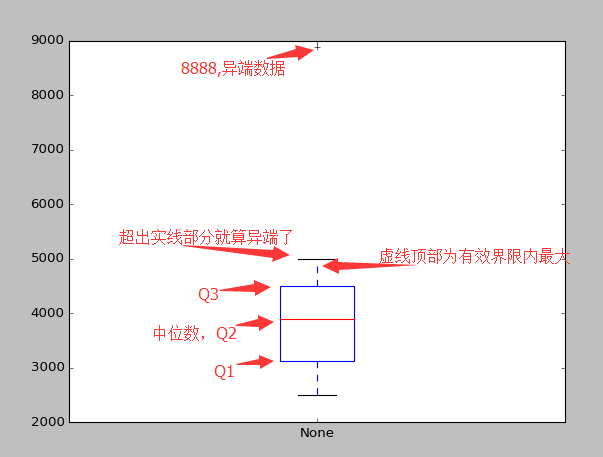
所以这里再说一下最后一种图形:箱线图:非常简单说一下箱线图的画法,说了肯定不懂,你懂不用我说,备忘用。
- 画箱体,坐标为Q1 - Q3 (第一个四分位到第三个四分位数)
- 在箱体中间,的中位数位置,画一条线把箱体分开
- 命IQR = Q3 - Q1 ,那么左右两边的界限坐标则为 Q1 - 1.5xIQR,Q2 + 1.5xIQR
- 在界限范围内,最小值与最大值的坐标位,用虚线与箱体相连
- 界限外的数据则认为是异端数据,在相应的坐标位置用虚线表示
那么,再用python画出刚才我们公司的工资情况的箱线图,由于100W太大,为了不让我的图上箱子的大小太细,换个小点的数,8888,在一群3000左右的工资里面也算异端了
datas = pd.Series([2500,3000,3000,3500,3800,4000,4500,4500,5000,8888])
# 打印这些值
q1 = datas[:5].median()
q2 = datas.median()
q3 = datas[5:].median()
iqr = q3 - q1
print q1
print q2
print q3
print iqr
# 画箱线图
datas.plot(kind='box')
plt.show()
z-分数(z-score)
简单点说z分数就是和平均数隔了几个标准差的距离。
- Z-分数: $z_i = \frac{x_i-\overline{x}}{s} $
- 切比雪夫定理: 与平均数的距离在z个标准差之内的数据值所占比例至少为$(1-1/z^2)$,其中z是大于1的任意实数
经验法则
经验法则这个名字太形象了,又叫68-95-99.7法则,名字想表述的是,当你没有电脑,没有计算器时,都可以凭借经验法则去完成一些判断,非常实用。
z-分数是用来描述分布形态的一个数,经验上的法则:
- 大约有68% 的数据值与平均数在一个标准差内
- 大约有95% 的数据与平均数的距离在2个标准差内
- 几乎所有的数据与平均数的距离在3个标准差之内
协方差、相关系数、加权平均数
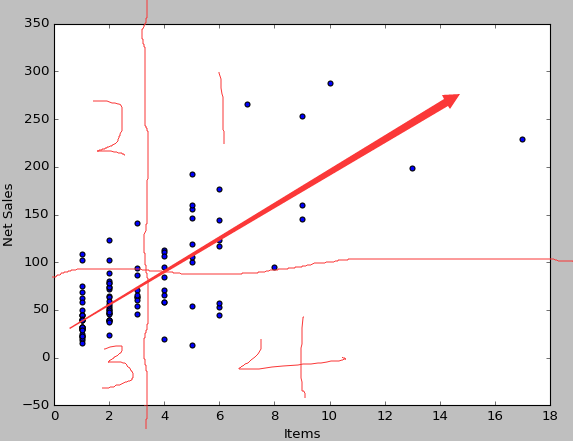
协方差一般都是用来研究两个变量的相关性关系,经常与上次说的散点图一起使用,对相关性做出更科学的解释,把上次的散点图再拿出来:再算出Items的平均数为3.2件,销售额平均为78元,则可以在图上标记出来,画出两条线分为4个象限,1、3象限为正,2、4象限为负,那么,一眼可以看出来正多于负,那么就是购买件数与销售额正相关,如下:
- 样本协方差 $s_{xy} = \frac{\sum{\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}}{n-1} $
- 总体协方差 $\sigma_{xy} = \frac{\sum{\left(x_i-\mu_x\right)\left(y_i-\mu_y\right)}}{n-1} $
- 样本相关系数 $ r_{xy} = \frac{s}{s_xs_y} $
- 总体相关系数 $ R_{xy} = \frac{\sigma}{\sigma_xs_y} $
- 加权平均数$\overline{x} = \frac{\sum{x_i}}{n} = \frac{x_1+x_2+x_3+\cdots + x_n}{n} $
- 加权平均数$\overline{x} = \frac{\sum{w_ix_i}}{\sum{w_i}} $
- 分组数据的样本平均数 $ \overline{x} = \frac{\sum{\int_iM_i}}{n} $
- 分组数据的样本方差 $s^2 = \frac{\sum{\int_i\left(M_i-\overline{x}\right)^2}}{N} $
- 分组数据的总体平均数$\mu = \frac{\sum{\int_iM_i}}{n} $
- 分组数据的总体方差$\sigma^2 = \frac{\sum{\int_i\left(M_i-\mu\right)^2}}{N} $
- 偏度 $\frac{n}{\left(n-1\right)\left(n-2\right)}\sum\left(\frac{x_i-\overline{x}}{s}\right)^3 $
协方差可以用 np.cov(arr1,arr2),此函数会返回二维数组 : [ [arr1的样本方差,协方差] [协方差,arr2的样本方差] ],所以相关系数也可以根据第0行的1列或1行0列去算
# 协方差
tmp = np.cov(data1,data2);
# 相关系数
tmp[0,1]/(np.sqrt(tmp[0,0])*np.sqrt(tmp[1,1]))
后面的加权平均数,方差等,是两个维度的计算,比如我花 10000 以10块的价格买了1000股,然后股票跌到了5块,我再花10000,买了2000股。
这时的平均数不是 (10+5)/2 = 7.5 ,而是 (20000/3000)=6.66 6.66是平均每股的成本,把数量也算上了,就是加权平均数,后面的总体平均数,方差等,都是加权进行计算,不多赘述了。
话外:除了Python,个人推荐简单的问题都以用Excel解决,很多人说Excel落伍,但个人觉得每种工具有每种工具的特性,Excel内置的各种统计函数,输入输出非常方便,是做简单分析的不错工具。